By just downloading file from www.kicsitbugs.weebly.com you can install this file.
Sunday, December 04, 2011
Thursday, October 13, 2011
Home LAN: Do you have home LAN
I have no such a home network but if I make it then first I would be control its administration.
So that I would use middle room or TV lounge and control all others room by centrally connected to my computer and my computer give privliges to other computers so that whether they can install any software or not.
So that I would use middle room or TV lounge and control all others room by centrally connected to my computer and my computer give privliges to other computers so that whether they can install any software or not.
Projectors: Which technology LCD or DLP projectors is Used
 |
| In view sonic LCD technology used |
LCD (liquid crystal display) projectors contain three separate LCD glass panels, one each for the red, green, and blue components of the video signal. Each LCD panel contains thousands (or millions) of liquid crystals that can be aligned in either open, closed, or partially closed positions to allow light to pass through. Each liquid crystal behaves in essence like a shutter or blind, and each represents a single pixel ("picture element"). As red, green, and blue light passes through the respective LCD panels, the liquid crystals open and close based on how much of each color is needed for that pixel at that moment in time. This activity modulates the light and produces the image that is projected onto the screen.
DLP ("Digital Light Processing") is a proprietary technology developed by Texas Instruments. It works quite differently than LCD. Instead of having glass panels through which light is passed, the DLP chip is a reflective surface made up of thousands (or millions) of tiny mirrors. Each mirror represents a single pixel.
In a DLP projector, light from the projector's lamp is directed onto the surface of the DLP chip. The mirrors tilt back and forth, directing light either into the lens path to turn the pixel on, or away from the lens path to turn it off.
In the most expensive DLP projectors, there are three separate DLP chips, one each for the red, green, and blue channels. However, in most DLP projectors under $10,000 there is only one chip. To define color, a color wheel is used that contains (at minimum) a red, green, and blue filter. This wheel spins in the light path between the lamp and the DLP chip and alternates the color of the light hitting the chip from red to green to blue. The mirrors tilt away from or into the lens path based upon how much of each color is required for each pixel at any given moment in time. This activity modulates the light and produces the image that is projected onto the screen.
Technology that we use in our class rooms
The technology that we use in classrooms is usually LCD which are usually view sonic used.
On the basis of lens or mirror we can check our projector is DLP or LCD
Is Image Clear In the back of class room
Some how image is clear This Question is left for back benchers :)
It is better than writing on white board so that it saves our time.
Voice recognition : Major problems and improvements
Major Problems In Voice Recognition:
Many challenges affect its accuracy. These include poor-quality voice samples; the variability in a speaker's voice due to illness, mood, changes over time; background noise as the caller interacts with the system; and changes in the call's technology (digital vs. analogue, upgrades to circuits and microphones, etc).
How they can be overcome:
A standard application programming interface (API) to reduce the issues with cost, interoperability, time-to-deployment, vendor lock-in, and other aspects of building applications, "So far, law enforcement, telecommunications services, and financial services in different countries, are using speaker verification but an API standard will make it easier and more attractive for integrators and others."
Many challenges affect its accuracy. These include poor-quality voice samples; the variability in a speaker's voice due to illness, mood, changes over time; background noise as the caller interacts with the system; and changes in the call's technology (digital vs. analogue, upgrades to circuits and microphones, etc).
How they can be overcome:
A standard application programming interface (API) to reduce the issues with cost, interoperability, time-to-deployment, vendor lock-in, and other aspects of building applications, "So far, law enforcement, telecommunications services, and financial services in different countries, are using speaker verification but an API standard will make it easier and more attractive for integrators and others."
Wednesday, October 12, 2011
Devices that are alternative to mouse
 Following devices can be used as a alternative to mouse.
Following devices can be used as a alternative to mouse.2. Laptop touch-pad
3. Track balls
4. Joy sticks
5. Roller ball
Have you used Ever?
Yes, not all but only mouse,joysticks and pen or stylus.
Which I prefer
I prefer to use pen or stylus but it has its own value .However in Gaming joystick is more reliable than mouse.
Why:
Mouse has its own value but in Gaming joysticks has more options than mouse and it is more effective in gaming tricks.
Saturday, October 08, 2011
Operating System Vocabulary
Operating
System Vocabulary Words
- Operating system - (OS)
The low-level software that handles the interface to peripheral hardware,
schedules tasks, allocates storage, and presents a default interface to
the user when no application
program is running.
- User Interface - The
aspects of a computer system or program which can be seen (or heard or
otherwise perceived) by the human user, and the commands and mechanisms
the user uses to control its operation and input data.
- Graphical User
Interface - (GUI) The use of pictures rather than just words to represent
the input and output of a program. A program with a GUI runs under some windowing
system (e.g. The X
Window System, Microsoft
Windows, Acorn
RISC OS,
NEXTSTEP).
The program displays certain icons, buttons, dialogue
boxes etc. in its windows on
the screen and the user controls it mainly by moving a pointer on
the screen (typically controlled by a mouse) and
selecting certain objects by pressing buttons on the mouse while the
pointer is pointing at them.
- Desktop - In graphical
user interfaces, a desktop is the metaphor used to portray file
systems. Such a desktop consists of pictures, called icons, that show
cabinets, files, folders, and
various types of documents
(that is, letters, reports, pictures).
- Icons - A small picture
intended to represent something (a file, directory, or action) in a graphical
user interface.
- Start button – button
usually in the bottom left hand side of an operating system windows 95 and
up
- Multitasking - A
technique used in an operating
system for sharing a single processor between several independent
jobs.
- Task switching - Refers
to operating
systems or operating
environments that enable you to switch from one program to another
without losing your spot in the first program. Many utilities are
available that add task switching to DOS systems.
- Active window – Refers
to objects
currently being displayed or used. For example, in graphical
user interfaces, the active window is the
window currently receiving mouse and keyboard input.
- Title bar - A bar on
top of a window.
The title bar contains the name of the file or application.
- File- A collection of data or information
that has a name,
called the filename
- Folder - In graphical
user interfaces such as Windows and the Macintosh
environment,
a folder is an object
that can contain multiple documents.
- Maximize - In graphical
user interfaces, to enlarge a window to its
maximum size.
- Minimize - In graphical
user interfaces, to convert a window into an icon.
- Restore - In graphical
user interfaces, to restore means to return a window to its
original size
- Extensions – filename
extension – the type of file that the file is
- Window - An enclosed,
rectangular area on a display screen.
Most modern operating
systems and applications
have graphical
user interfaces that let you divide your display into several windows.
- Taskbar – menu bar,
which is usually at the bottom of the windows operating system, which most
programs running, appears in.
- Pull down menu – A menu in a graphical
user interface, whose title is normally visible but whose contents are
revealed only when the user activates it
- Menu Bar - A
permanently displayed menu spread
horizontally across the top of the screen or window. When the mouse is
pressed over an item on the menu bar, a pull-down
menu appears.

Sunday, October 02, 2011
Information System & Information Technology
Information Systems
® Information systems are implemented within an organization
® For improving the effectiveness and efficiency of that organization.
® Capabilities of the information system and characteristics of the organization, its work systems, its people, and its development and implementation methodologies together determine the extent to which that purpose is achieved.
Information Systems
- The branch of engineering that deals with the use of computers and telecommunications to retrieve and store and transmit information.
- The term "IT" encompasses the methods and techniques used in information handling and retrieval by automatic means.
- The means include computers, telecommunications and office systems or any combination of these elements.
- The industry or discipline involving the collection, dissemination, and management of data, typically through the use of computers.
- Technology tasked with processing, storing and communication of information e.g. computers, mobile phones, PDA’s.
Computer Software
- Computer software, or just software, is the collection of computer programs and related data that provide the instructions telling a computer what to do.
- Software is intangible, meaning it "cannot be touched".
- Examples of computer software :
- Application software includes end-user applications of computers such as word processors or Video games, and ERP software for groups of users.
- System software is computer software designed to operate the computer hardware and to provide and maintain a platform for running application software.
Multi-Processing & Multi-Tasking
Multi-Processing
- Multiprocessing is the use of two or more central processing units (CPUs) within a single computer system.
- The term also refers to the ability of a system to support more than one processor and/or the ability to allocate tasks between them.
- There are many variations on this basic theme, and the definition of multiprocessing can vary with context, mostly as a function of how CPUs are defined (multiple cores on one die, multiple dies in one package, multiple packages in one system unit, etc.).
- Multiprocessing sometimes refers to the execution of multiple concurrent software processes in a system as opposed to a single process at any one instant.
- However, the terms multitasking or multiprogramming are more appropriate to describe this concept, which is implemented mostly in software.
- In computing, multitasking is a method by which multiple tasks, also known as processes, share common processing resources such as a CPU.
- In the case of a computer with a single CPU, only one task is said to be running at any point in time, meaning that the CPU is actively executing instructions for that task.
- Multitasking solves the problem by scheduling which task may be the one running at any given time, and when another waiting task gets a turn. The act of reassigning a CPU from one task to another one is called a context switch.
- When context switches occur frequently enough the illusion of parallelism is achieved. Even on computers with more than one CPU (called multiprocessor machines), multitasking allows many more tasks to be run than there are CPUs.
 |
| Add caption |
Computer Hardware
- Your PC (Personal Computer) is a system, consisting of many components.
- Some of those components, like Windows XP, and all your other programs, are software.
- The stuff you can actually see and touch, and would likely break if you threw is hardware.
Hardware of a modern Personal Computer.
o Monitor
o Motherboard
o CPU
o RAM
o Expansion cards
o Hard disk drive
o Keyboard & Mouse
Computer Software
- Computer software, or just software, is the collection of computer programs and related data that provide the instructions telling a computer what to do.
- Software is intangible, meaning it "cannot be touched".
- Examples of computer software :
- Application software includes end-user applications of computers such as word processors or Video games, and ERP software for groups of users.
- System software is computer software designed to operate the computer hardware and to provide and maintain a platform for running application software.
History of Computers
Computers were initially large machines that could fill entire rooms. Some were operated using large vacuum tubes that formed the basis of today's transistors. In order to operate such machines, punch cards were used. One of the first such examples of this was the Jacquard Loom.
- In 1833 Charles Babbage invented his difference engine, an early calculator.
- Together with the punch card design, he created the analytical engine.
- Here are some computers that came and went in the history of computing.
® ENIAC
- A behemoth of a machine weighing 27 tones, ENIAC stood for Electrical Numerical Integrator and Computer.
- The ENIAC used thousands of vacuum tubes and a punch card mechanism.
- It was originally used to perform calculations for the hydrogen bomb, and later saw use in calculating artillery firing tables.
- Working out the programming on paper took weeks, and performing the necessary wiring took days. The ENIAC saw service until October 2, 1955.
® Macintosh
· First introduced by Apple in 1984, the Macintosh was the first computer to use a mouse and graphical user interface (GUI) rather than a command line interface.
· However due to the immense cost of porting command line interface programs to the GUI, software development was initially slow.
· In this computer maintained as the basis level of the computer.
Saturday, October 01, 2011
inequality
Basic Rules
In this section, you will learn how so solve inequalities. "Solving'' an inequality means finding all of its solutions. A "solution'' of an inequality is a number which when substituted for the variable makes the inequality a true statement.
Here is an example: Consider the inequality
When we substitute 8 for x, the inequality becomes 8-2 > 5. Thus, x=8 is a solution of the inequality. On the other hand, substituting -2 for x yields the false statement (-2)-2 > 5. Thus x = -2 is NOT a solution of the inequality. Inequalities usually have many solutions.
As in the case of solving equations, there are certain manipulations of the inequality which do not change the solutions. Here is a list of "permissible'' manipulations:
- Rule 1. Adding/subtracting the same number on both sides.Example: The inequality x-2>5 has the same solutions as the inequality x > 7. (The second inequality was obtained from the first one by adding 2 on both sides.)
- Rule 2. Switching sides and changing the orientation of the inequality sign.Example: The inequality 5-x> 4 has the same solutions as the inequality 4 < 5 - x. (We have switched sides and turned the ``>'' into a ``<'').
- Rule 3a. Multiplying/dividing by the same POSITIVE number on both sides.
- Rule 3b. Multiplying/dividing by the same NEGATIVE number on both sides AND changing the orientation of the inequality sign.Examples: This sounds harmless enough. The inequality
 has the same solutions as the inequality
has the same solutions as the inequality  . (We divided by +2 on both sides). The inequality -2x > 4 has the same solutions as the inequality x< -2. (We divided by (-2) on both sides and switched ">'' to "<''.) But Rule 3 prohibits fancier moves: The inequality
. (We divided by +2 on both sides). The inequality -2x > 4 has the same solutions as the inequality x< -2. (We divided by (-2) on both sides and switched ">'' to "<''.) But Rule 3 prohibits fancier moves: The inequality  DOES NOT have the same solutions as the inequality x > 1. (We were planning on dividing both sides by x, but we can't, because we do not know at this point whether x will be positive or negative!) In fact, it is easy to check that x = -2 solves the first inequality, but does not solve the second inequality.
DOES NOT have the same solutions as the inequality x > 1. (We were planning on dividing both sides by x, but we can't, because we do not know at this point whether x will be positive or negative!) In fact, it is easy to check that x = -2 solves the first inequality, but does not solve the second inequality.
Let's solve some inequalities:
Example 1:
Consider the inequalityThe basic strategy for inequalities and equations is the same: isolate x on one side, and put the "other stuff" on the other side. Following this strategy, let's move +5 to the right side. We accomplish this by subtracting 5 on both sides (Rule 1) to obtain
after simplification we obtain
Once we divide by +2 on both sides (Rule 3a), we have succeeded in isolating x on the left:
or simplified,
All real numbers less than 1 solve the inequality. We say that the "set of solutions'' of the inequality consists of all real numbers less than 1. In interval notation, the set of solutions is the interval
Example 2:
Find all solutions of the inequalityLet's start by moving the ``5'' to the right side by subtracting 5 on both sides (Rule 1):
or simplified,
How do we get rid of the ``-'' sign in front of x? Just multiply by (-1) on both sides (Rule 3b), changing "
or simplified
All real numbers greater than or equal to -1 satisfy the inequality. The set of solutions of the inequality is the interval
Example 3:
Solve the inequalityLet us simplify first:
There is more than one route to proceed; let's take this one: subtract 2x on both sides (Rule 1).
and simplify:
Next, subtract 9 on both sides (Rule 1):
simplify to obtain
Then, divide by 4 (Rule 3a):
and simplify again:
It looks nicer, if we switch sides (Rule 2).
In interval notation, the set of solutions looks like this:
 .
.Exercise 1:
Find all solutions of the inequalityAnswer.
Exercise 2:
Solve the inequalityAnswer.
Exercise 3:
Solve the inequalityAnswer.
Exercise 4:
Find all solutions of the inequalityAnswer.
modulus
Definition
The absolute value (or modulus) of a real number x is x's numerical value without regard to its sign.
of a real number x is x's numerical value without regard to its sign.
For example, ;
;  ;
; 
Graph:
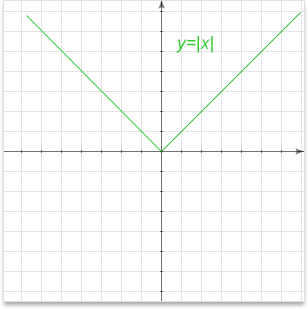
Important properties:





3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
For example,
a) Positive: if , we can rewrite the equation as:
, we can rewrite the equation as: 
b) Negative: if , we can rewrite the equation as:
, we can rewrite the equation as: 
We can also think about conditions like graphics. is a key point in which the expression under modulus equals zero. All points right are the first conditions
is a key point in which the expression under modulus equals zero. All points right are the first conditions  and all points left are second conditions
and all points left are second conditions  .
.
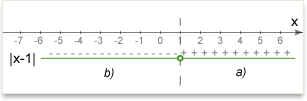
2. Solve new equations:
a) --> x=5
--> x=5
b) --> x=-3
--> x=-3
3. Check conditions for each solution:
a) has to satisfy initial condition
has to satisfy initial condition  .
.  . It satisfies. Otherwise, we would have to reject x=5.
. It satisfies. Otherwise, we would have to reject x=5.
b) has to satisfy initial condition
has to satisfy initial condition  .
.  . It satisfies. Otherwise, we would have to reject x=-3.
. It satisfies. Otherwise, we would have to reject x=-3.
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.: . How many solutions does the equation have?
. How many solutions does the equation have?
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a) .
.  -->
-->  . We reject the solution because our condition is not satisfied (-1 is not less than -8)
. We reject the solution because our condition is not satisfied (-1 is not less than -8)
b) .
.  -->
-->  . We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
. We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
c) .
.  -->
-->  . We reject the solution because our condition is not satisfied (-15 is not within (-3,4) interval.)
. We reject the solution because our condition is not satisfied (-15 is not within (-3,4) interval.)
d) .
.  -->
-->  . We reject the solution because our condition is not satisfied (-1 is not more than 4)
. We reject the solution because our condition is not satisfied (-1 is not more than 4)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
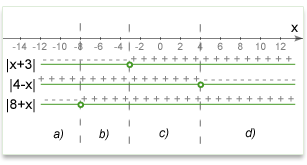
Answer: 0
Example #2
Q.: . What is x?
. What is x?
Solution: There are 2 conditions:
a) -->
-->  or
or  .
.  -->
-->  . x e {
. x e { ,
,  } and both solutions satisfy the condition.
} and both solutions satisfy the condition.
b) -->
-->  .
.  -->
-->  . x e {
. x e { ,
,  } and both solutions satisfy the condition.
} and both solutions satisfy the condition.
(Optional) The following illustration may help you understand how to open modulus at different conditions.
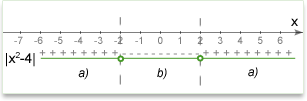
Answer: ,
,  ,
,  ,
, 
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?

A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
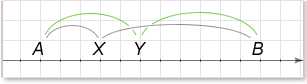
We can think about absolute values here as distance between points. Statement 1 means than distance between Y and A is less than Y and B. Because X is between A and Y, distance between |X-A| < |Y-A| and at the same time distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring third step in opening modulus - always check whether your solution satisfies conditions.
Official GMAC Books:
The Official Guide, 12th Edition: PS #22; PS #50; PS #130; DS #1; DS #153;
The Official Guide, Quantitative 2th Edition: PS #152; PS #156; DS #96; DS #120;
The Official Guide, 11th Edition: DT #9; PS #20; PS #130; DS #3; DS #105; DS #128;
Generated from [GMAT ToolKit]
Resources
Absolute value DS problems: [search]
Absolute value PS problems: [search]
Fig's post with absolute value problems: [Absolute Value Problems]
For more information click here
The absolute value (or modulus)
For example,
Graph:
Important properties:
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
- Positive (or rather non-negative)
- Negative
For example,
a) Positive: if
b) Negative: if
We can also think about conditions like graphics.
2. Solve new equations:
a)
b)
3. Check conditions for each solution:
a)
b)
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.:
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a)
b)
c)
d)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer: 0
Example #2
Q.:
Solution: There are 2 conditions:
a)
b)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer:
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?
A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
We can think about absolute values here as distance between points. Statement 1 means than distance between Y and A is less than Y and B. Because X is between A and Y, distance between |X-A| < |Y-A| and at the same time distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring third step in opening modulus - always check whether your solution satisfies conditions.
Official GMAC Books:
The Official Guide, 12th Edition: PS #22; PS #50; PS #130; DS #1; DS #153;
The Official Guide, Quantitative 2th Edition: PS #152; PS #156; DS #96; DS #120;
The Official Guide, 11th Edition: DT #9; PS #20; PS #130; DS #3; DS #105; DS #128;
Generated from [GMAT ToolKit]
Resources
Absolute value DS problems: [search]
Absolute value PS problems: [search]
Fig's post with absolute value problems: [Absolute Value Problems]
For more information click here
Subscribe to:
Comments (Atom)






