Definition
The absolute value (or modulus)
of a real number x is x's numerical value without regard to its sign.
For example,
; 
; 
Graph:
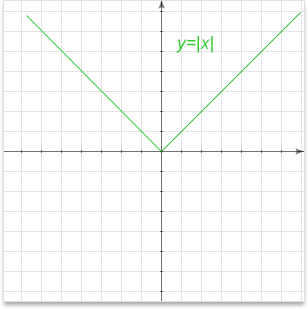
Important properties:
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
For example,
a) Positive: if
, we can rewrite the equation as: 
b) Negative: if
, we can rewrite the equation as: 
We can also think about conditions like graphics.
is a key point in which the expression under modulus equals zero. All points right are the first conditions 
and all points left are second conditions 
.
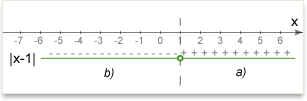
2. Solve new equations:
a) --> x=5
b)
--> x=-3
3. Check conditions for each solution:
a)
has to satisfy initial condition 
. 
. It satisfies. Otherwise, we would have to reject x=5.
b)
has to satisfy initial condition 
. 
. It satisfies. Otherwise, we would have to reject x=-3.
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.:
. How many solutions does the equation have?
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a)
. 
--> 
. We reject the solution because our condition is not satisfied (-1 is not less than -8)
b)
. 
--> 
. We reject the solution because our condition is not satisfied (-15 is not within (-8,-3) interval.)
c)
. 
--> 
. We reject the solution because our condition is not satisfied (-15 is not within (-3,4) interval.)
d)
. 
--> . We reject the solution because our condition is not satisfied (-1 is not more than 4)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
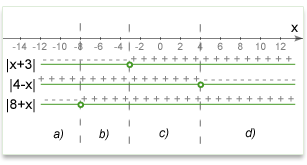
Answer: 0
Example #2
Q.:
. What is x?
Solution: There are 2 conditions:
a)
--> 
or 
. 
--> 
. x e {
, 
} and both solutions satisfy the condition.
b)
--> 
. 
--> 
. x e {
, 
} and both solutions satisfy the condition.
(Optional) The following illustration may help you understand how to open modulus at different conditions.
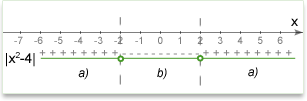
Answer:, , ,
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?
A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
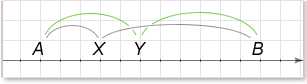
We can think about absolute values here as distance between points. Statement 1 means than distance between Y and A is less than Y and B. Because X is between A and Y, distance between |X-A| < |Y-A| and at the same time distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring third step in opening modulus - always check whether your solution satisfies conditions.
Official GMAC Books:
The Official Guide, 12th Edition: PS #22; PS #50; PS #130; DS #1; DS #153;
The Official Guide, Quantitative 2th Edition: PS #152; PS #156; DS #96; DS #120;
The Official Guide, 11th Edition: DT #9; PS #20; PS #130; DS #3; DS #105; DS #128;
Generated from [GMAT ToolKit]
Resources
Absolute value DS problems: [search]
Absolute value PS problems: [search]
Fig's post with absolute value problems: [Absolute Value Problems]
For more information click here
The absolute value (or modulus)
For example,
Graph:
Important properties:
3-steps approach:
General approach to solving equalities and inequalities with absolute value:
1. Open modulus and set conditions.
To solve/open a modulus, you need to consider 2 situations to find all roots:
- Positive (or rather non-negative)
- Negative
For example,
a) Positive: if
b) Negative: if
We can also think about conditions like graphics.
2. Solve new equations:
a)
b)
3. Check conditions for each solution:
a)
b)
3-steps approach for complex problems
Let’s consider following examples,
Example #1
Q.:
Solution: There are 3 key points here: -8, -3, 4. So we have 4 conditions:
a)
b)
c)
d)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer: 0
Example #2
Q.:
Solution: There are 2 conditions:
a)
b)
(Optional) The following illustration may help you understand how to open modulus at different conditions.
Answer:
Tip & Tricks
The 3-steps method works in almost all cases. At the same time, often there are shortcuts and tricks that allow you to solve absolute value problems in 10-20 sec.
I. Thinking of inequality with modulus as a segment at the number line.
For example,
Problem: 1<x<9. What inequality represents this condition?
A. |x|<3
B. |x+5|<4
C. |x-1|<9
D. |-5+x|<4
E. |3+x|<5
Solution: 10sec. Traditional 3-steps method is too time-consume technique. First of all we find length (9-1)=8 and center (1+8/2=5) of the segment represented by 1<x<9. Now, let’s look at our options. Only B and D has 8/2=4 on the right side and D had left site 0 at x=5. Therefore, answer is D.
II. Converting inequalities with modulus into range expression.
In many cases, especially in DS problems, it helps avoid silly mistakes.
For example,
|x|<5 is equal to x e (-5,5).
|x+3|>3 is equal to x e (-inf,-6)&(0,+inf)
III. Thinking about absolute values as distance between points at the number line.
For example,
Problem: A<X<Y<B. Is |A-X| <|X-B|?
1) |Y-A|<|B-Y|
Solution:
We can think about absolute values here as distance between points. Statement 1 means than distance between Y and A is less than Y and B. Because X is between A and Y, distance between |X-A| < |Y-A| and at the same time distance between X and B will be larger than that between Y and B (|B-Y|<|B-X|). Therefore, statement 1 is sufficient.
Pitfalls
The most typical pitfall is ignoring third step in opening modulus - always check whether your solution satisfies conditions.
Official GMAC Books:
The Official Guide, 12th Edition: PS #22; PS #50; PS #130; DS #1; DS #153;
The Official Guide, Quantitative 2th Edition: PS #152; PS #156; DS #96; DS #120;
The Official Guide, 11th Edition: DT #9; PS #20; PS #130; DS #3; DS #105; DS #128;
Generated from [GMAT ToolKit]
Resources
Absolute value DS problems: [search]
Absolute value PS problems: [search]
Fig's post with absolute value problems: [Absolute Value Problems]
For more information click here
